発達の科学

発達研究を目指す人へ

　認知発達の研究者を志す者に、私たちの研究室ではどのような研究をしているのか、どのような学生に来てほしいと思っているのか、認知発達研究者になるためにはどのような資質が要求されるのか等々に関して、 Q&A式に書いてみます。皆さんがこの記事を読んだことをきっかけに、子どもの認知発達に興味を持ち、当研究室の研究活動に参加されんことをこころから期待しています。心当たりのある学生、志のある方は、是非チャレンジしてみてください。

なお、皆さんの中に、この研究室について知りたいこと、尋ねたいことがありましたらメールをください。今後、皆さんの問い合わせを参考にQ&Aの項目を追加していくつもりです。

Q1「この研究室では、どんなことが研究できるのでしょうか？」
Q2「子どもの認知発達というと、幼稚園児、小学生児童だけを研究しているのですか？」
Q3「この研究室にどのような学生が来ることを期待しているのですか？」、「私は心理学を専攻していないのですが、この研究室で研究できるのでしょうか？」
Q4「認知発達現象に対して強い好奇心を持つこととありましたが、認知発達に関してそんなに面白い研究ができるのでしょうか？」

Q1 「この研究室では、どんなことが研究できるのでしょうか？」

A1 　
当研究室では、子どもの認知発達について研究しています。認知発達研究といっても非常に広い範囲をカバーしています。認知の内容という観点から言えば、子どもにおける生物学的認識、物理学的認識、心理学的認識、道徳・慣習的認識、社会的認識（自己・他者認識を含む）、政治・経済的認識、歴史的認識、言語・象徴認識、論理・数学的認識、空間・時間的認識などがいかに獲得されていくのか、その獲得過程を如何に説明するのかを研究しています。もちろん子どもは科学的認識と呼べるような考え方をまだ持っていません。しかし、将来的に科学的認識につながるにせよ、つながらないにせよ、幼児は幼児なりに素朴な認識を幼児でも持っています。幼児の生物学的認識、物理学的認識については、「素朴生物学」、「素朴物理学」、心理学的認識については「心の理論」などとも呼ばれています。このような素朴な考え方がどのようなものであるかを明らかにし、それが如何にして科学的認識につながっていくのかを研究しています。一方、このような認識を獲得するためには、様々な認知的道具が必要です。従って、子どもの認識獲得を支える心的諸機能という観点から言えば、表象機能、学習機能、記憶機能、メタ認知機能、推論機能、実行機能などの発達も当研究室の重要な研究課題となります。表象機能には言語ばかりでなく、描画、心像、模倣なども含まれます。このような心的機能の発達はそれ自体が研究対象であるばかりでなく、素朴理論あるいは科学的認識の獲得においてそれらが果たす役割という観点も重要な研究テーマとなるでしょう。

要するに、当研究室でやっていることは、子どもの認識内容であれ認知機能であれ、人間精神の発達という神秘のヴェールを剥いでいく営みです。もう少し具体的な例でいえば、幼児に「嘘をつく」とはどういうことかを尋ねてみましょう。幼稚園児なら「悪い言葉を口に出すこと」と答えるでしょう。「悪い言葉」とは日本語の場合、「馬鹿」とか「こん畜生」と言った言葉です。「嘘とは相手をだます意図で、本当でないことをいうこと」という、大人の嘘の定義から随分かけ離れた考え方ですね。そこで疑問が生じます。幼児は何故、「嘘とは口にしてはいけないような悪い言葉をいうこと」と考えるのでしょうか。子どもが悪い言葉を口にしたとき、親から「そんな嘘をついてはいけません」と言われたことはないでしょうから、経験によってこのような考え方を持つようになったとは説明することは出来ませんね。親からこのような嘘の定義を一度も聞いたはずがないにも関わらず、何故このような考え方を懐くのでしょうか。また、このような考え方から一足飛びに大人の考え方に、あるとき突如移行すると考えることも難しいですね。幼児の嘘の定義と大人のそれとはあまりにもかけ離れているのですから。それでは幼児の考え方から、いつごろ、どのようなプロセスを経て、大人の考え方を身につけるようになるのでしょうか。さらに、この考え方の漸進的移行をどのように説明すればいいのでしょうか。「嘘をつくとはどういうことか？」という道徳的認識に関わる一つの問から、次々と色々な疑問が生じてきます。このような疑問を実証的調査と理論的考察を踏まえながら、子どもの精神発達の神秘を解明していくという研究をやっているわけです。

Q2 「子どもの認知発達というと、幼稚園児、小学生児童だけを研究しているのですか？」

A2
発達心理学と言うのは、精神現象をその発達という観点から解明しようとする学問です。したがって、発達研究というのは特定の年齢層だけを研究対象にするものではありません。幼児だけ、児童だけを研究対象にするのであれば、それぞれを幼児心理学、児童心理学と呼び、発達心理学と区別されます。発達調査の対象者という観点から言えば、現在のところ当研究室では言葉を話し始める2,3歳以降の幼児期から児童期、青年期を経て大人に至るまでの認知発達を研究しています。といっても、どの研究課題についてもこれだけの広範囲をカバーして調査しているわけではありません。一般的には、研究課題に関して最も顕著な発達が見られる時期を中心に調査を行ないます。計数（counting）の認識であれば、幼児期中心の調査になるでしょうし、命題的推論であれば、中学生から高校生、大学生にいたる青年期が中心になるでしょう。当研究室ではまだ実施したことはありませんが、もし乳児の認知発達研究をやりたい方があれば乳児期を、加齢による認知的後退を研究したいのであれば、老齢期をもちろん調査することになります。ですから乳児期、老齢期を研究したい方も大歓迎です。しかし、いずれの年齢層を研究対象とするにせよ、すべての精神現象を発達の相において見るというのが当研究室の根本的姿勢といえるでしょう。

Q3「この研究室にどのような学生が来ることを期待しているのですか？」、「私は心理学を専攻していないのですが、この研究室で研究できるのでしょうか？」

A3
この研究室で研究するのに必要な最少限の資質は次の二つです。

１　認知発達現象に対して強い好奇心を持っていること
２　研究に必要な技術を習得できるだけの学力を有すること。

1についてはコメントする必要もないでしょう。学問研究の一次的動機づけが研究すること自体の面白さにあるわけですから、認知発達研究においては認知発達現象に対して強い興味を持っていることが不可欠な要件です。応用的、あるいは、実利的目的から認知発達に関心を持ったにしても、認知発達現象そのものに興味が持てないのであれば、ここで研究することは向かないでしょう。二次的動機づけで行なっているような研究は持続しないいし、第三者から見ても面白くない研究になってしまいます。しかし、たとえ応用的、実利的目的から関心を持ったにしても、それをきっかけとして発達現象そのものが面白いと感じるのであれば、大いに歓迎したいと思います。

２については少し注釈が必要です。「研究に必要な技術」というのは、先行研究を知るための文献講読に関するもの、研究調査を行なうための調査法に関するもの、調査結果をまとめたり、分析したりするためのデータ処理法に関するもの等が考えられます。例えば、研究のために講読しなければならない文献はほとんどが英語論文ですから、英語が読めなければ話になりません。調査結果を論文としてまとめるためには、素データを何らかの形で処理しなければなりません。そのためには心理統計法を知っている必要があります。他にも研究に必要な技術は色々とありますが、重要なことは、このような「技術を習得していること」ではなく、「習得できるだけの学力を有すること」が必要な資質だという点です。つまり、当研究室に入ってくる時点で、研究に必要な技術を習得済みであることを要請していません。その習得が必要になった時点で習得できるだけの力があることを要請しているだけです。したがって、学部の専門が心理系でない学生の参加も大いに歓迎します。もちろん、心理系出身の学生のほうが、調査法やデータ処理に関して研究に必要な技術を既に習得している可能性が高いでしょうから、スタートダッシュが早くて研究を進めていく上で有利なことは確かでしょう。だからこそ、大学院入学試験で心理学に関する専門的知識が問われ、専門的知識のある人が優先的に入学を許されるわけです。しかし、研究者として一人前になれるかどうかは、入学時の専門知識の多少ではなく、研究に必要な技術を習得できるだけの力があるかどうかです。

　また、他学部出身の学生のほうが有利になる場合もあります。出身の学部で学んだ専門知識が認知発達研究に役立つことが大いにあるからです。例えば、子どもの経済的観念の発達を研究するため、同じ位の大きさの高級メロンとグレープフルーツを提示して、「メロンの方がグレープフルーツよりなぜ値段が高いのか」と小学生に聞いて見ることにしましょう。多くの子どもは「メロンの方がおいしいから」と答えるでしょう（田丸敏高著『子どもの発達と社会認識』京都・法政出版参照）。この種の理由を聞いて心理系出身の学生なら「子どもは食べ物の値段を味によって評価するのだ」と子どもの考えを要約するかもしれません。しかし経済学を勉強してきた学生なら、同じ理由をきいて「交換価値と使用価値の分化と関連付けに問題がある」と読み取ることが出来るでしょう。得られたデータが同じであっても、データ内容に関する専門知識がその読み取りに大いに影響し、専門知識に通じている者の方がより深く、より一般性のある読み取りが出来るのです。この意味において、認知発達研究は学際的研究であって、出身学部・学科が心理系である学生ばかりではなく、専門分野が心理系でない、理工系から社会・人文系に至るあらゆる分野の学生が、認知発達研究に積極的にチャレンジしていただきたいと思います。

Q4「認知発達現象に対して強い好奇心を持つこととありましたが、認知発達に関してそんなに面白い研究ができるのでしょうか？」

A4
認知発達現象に対する興味はあなた自身の認知システムとこれまでの経験に依存しているので、どんな現象であれ誰にとっても絶対的に面白い現象というものはありません。しかし、いくつかの事例を紹介しますから、皆さんの興味を引くかどうか、自問してみてください。なお、数の保存課題と差異予測課題とは、『ピアジェに学ぶ認知発達の科学』（北大路書房 2007）の中の小論「認知発達の科学のために」にもピアジェ理論の面白さとして紹介したことがあります。そこには課題の結果が示す認知発達理論上の意味についてもかかれていますので、興味のある方は見てください。

1　数の保存課題

実験者が子ども（4,5歳児）の前に、赤いおはじきと白いおはじきを6個ずつ平列するように並べる。2列のおはじきは、赤と白とが見た目にも対になって並べてあるので、列の長さもほぼ同じである（図1参照）。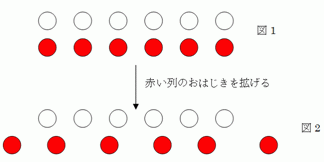

この状態で、子どもに「赤いおはじきと白いおはじき、どちらの方が数が多いですか、それとも同じ数だけありますか」と問うと、ほとんどの4,5歳児は赤いおはじきと白いおはじきとが同数であることを認める。次に子どもの見ている前で、実験者が一方のおはじき（図2では、赤いおはじき）を拡げてから、同じ質問をすると、同数あることを認めず、一般に広がった赤いおはじきの方が多いと主張する。「赤が多い!　だって、（赤い列の左端あるいは右端のおはじきを指差しながら）赤がここまで出ているから」というのが典型的な理由である。実験者が列を広げるところを子どもは見ており、おはじきをそこから取りさったり新たに付け加えたりしていないことを知っているにもかかわらず、数が増えたり減ったりすることを認めるのである。この課題は有名なピアジェ課題の一つで、「数の保存課題」と呼ばれています。数の保存原理（要素の個数は取りも付け加えもしなければ変わらないという原理）は、大人にとっては問うてみるまでもないほど自明な真理であっても、子どもにとっては自明な真理とはかぎらないということが分かります。

さらに、二つの集合が同数かどうかは数を数えれば分かることですから、図2の状態で、子どもに赤いおはじきと白いおはじきをかぞえさせて見ましょう。4,5歳にもなれば、計数できる子どもが多くなりますから、そのような子どもは赤白どちらも6個あることを認めるでしょう。そこで、もう一度「赤と白、どちらの方が多いの？」と数の保存課題の質問をします。するとそれでも子どもは一般に「赤のほうが多い」と答えます（もちろん、計数した後、保存判断する子どもも中にはいます）。つまり、「赤も白もどちらも６個ずつあるけれども、赤のほうが白よりが多い」と主張しているのです。子どもにとって集合の要素数を数えることとその集合の基数とは直接結びついていないことが分かります。

数の保存課題における非保存判断といい、数えることが基数の意味と結びつかないという考え方といい、幼児時代が遠い過去になってしまった皆さんには非常に理解しにくいことかもしれませんが、それだからこそ研究者にとっては新鮮な驚きであり、「何故なんだろう」という研究者の知的好奇心を掻きたてるのです。

2　差異予測課題

実験者は、図3のように視覚的に1対1対応に並べられた2列のおはじき（2列のおはじきは共に緑色で，列Aも列Bも5個ずつあるとする）を子ども（小学生1年生頃）に提示し，2列が同数であることをまず子どもに確かめる。次に，子どもの見ている前で、実験者が図4のように列Bより列Aに2個移動させる。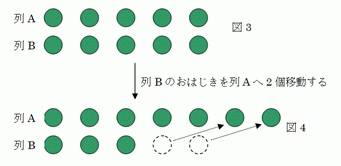

列Aの方が列Bより多くなったことを子どもに確認してから、「こちら（列A）はこちら（列B）よりいくつ多いのですか」と問うのが、差異予測課題である。しかし、移動後も何もしなければ、図4のように差異が見えてしまうので，差異読み取り課題となってしまう。そこで、いくつ移動させたかが分かるように，移動過程を見せるものの，移動させたあとは全体をカバーして2列とも見せないようにしてから差異予測課題と問う。

　この課題に対して，子どもは，「こっちは（列A）はこっちより（列B）よりも２個多い。だって2個動かしたのだから」と予測する。最初，5個ずつあったこと，移動後は列Aが2個増えて7個，列Bが2個減って3個になることを計算できても、一般にこのような予測をする。そこで、カバーを取って，２列の差異を確認させると差が4個になっていることを子どもは認めるものの，2個の移動がなぜ4個の差異を生むのか理解できない。子どもに敢えて説明を求めると，

（１）移動させるとき、（ひそかに）4個移動させたから，
（２）もともと列Aは列Bより（気づかれないように）2個多くしていたから，
（３）列Aへの2個の移動とは別に（ひそかに）列Bから2個取り去ったから，

という類の実に巧妙な合理化rationalizationを行なう。中には「ええ…4個も増えている。おじさん，インチキしちゃ駄目だよ！」という者さえいる。

種も仕掛けもない課題に対して，子どもが手品を見せられているかのように振舞うことほど，実験者にとって愉快なことはないであろう。単に愉快であるだけではなく、この実験の結果は子どもの思考様式について実に多くのことを考えさせてくれる。２＋２を計算できれば解決できそうな差異予測課題がなぜかくも難しいのか、単に予測が難しいだけでなく、移動後の状態（図４）を見せられても、4個の差異を生む理由を説明することがなぜかくも難しいのか、予測の誤りを説明するのに、既に確認した2個の移動と4個の差異とを関係づけようとするのではなく、なぜ確認していない要因に訴えて予測の誤りを合理化しようとするのか等々、次々と疑問が湧いてきます。

さらにこの課題をもっと年少児（4歳児位）でやってみると、年少児は移動後の差異の予測どころか、差異を読み取ること（差異読み取り課題）そのものが難しいということが分かってきます。例えば、図５のように、最初4個ずつから出発して、列Bから列Aへ一個移動させます。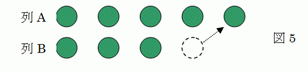

この課題は差異読み取り課題ですから、移動後もカバーをしません。すべてが見えています。列Bと列Aとはどちらが多いかを問くと、4歳児でももちろん列Aの方が多いと認めます。そこで、実験者が「こっち（列A）はこっち（列B）よりいくつ多いですか」と問うと、子どもは元気よく「こっち（列A）の方が5個多い！」と答えるのです。既に5個以上の計数ができる子を想定しているわけですから、差異2個の部分を読み取ることができないのでありません。要素の移動とは関係なしに、列Bと列Aのおはじきの色を変えて問うても結果は同じです。4歳児は一般に差異を尋ねる質問に対して、総数で答えてしまいます。不思議ですね。これはどうしてでしょうか、皆さん是非自分の頭で考えてみてください。

3　物の永続性課題

以下は、ホームで電車を待っている2歳児と母親との対話です。

・2歳児「ママ，電車ってけしごむ？」，
・母親「どうして？」，
・2歳児「だって，電車が行っちゃたら，あっちの（ホームの）人みんな消えてるよ」

という逸話があります（朝日新聞『あのね』 2000年7月7日朝刊）。

この逸話のどこが面白いのでしょうか。この点を学生に聞くと、多くは「電車が人を乗せて走り去るとホームには人がいなくなる様子を消しゴムが書かれた文字を消し去ることに喩えたもので、子どもらしいユニークな発想だ。」とか、「消しゴムと電車という大きさも形も大きく違うものを結び付けており、幼児は感性豊かな詩人だ」といった、比喩の巧みさに注目した回答をします。でもこれは比喩でしょうか。比喩であるなら、「電車ってけしごむ（みたい）だね」と肯定形で表現しそうなものなのに、子どもは「電車はけしごむですか？」と疑問形で、まじめに母親に質問しているのです。では、子どもにとって何が不可解なのでしょうか。子どもは、疑問点を自ら語っています。「電車が走り去ったあと、再び人が見えるはずなのに、なぜか消えてしまったこと」が理解できなかったのです。それでは、プラットホームの人が電車に乗り込むことを子どもが知らないだけのことでしょうか。ここで、「（ホームの人が）消えてるよ」と言っていることに注目してください。もし、ホームの人が電車に乗り込むことを子どもが知らないのであれば、「（ホームの人が）居なくなったよ」というはずです。「消える」と「居ない」とは大違いです。「居ない」は、ホームにいた人が現在どこか知らないけれどどこかにいることを想定しているのに対し、「消える」はそのような想定はありません。つまり、文字通り「電車が走り去ったあと、再び人が見えるはずなのに、見えなくなってしまった」ことに疑問を持ったと解釈せざるを得ません。この解釈が正しいとすると、物や人が障害物で一度隠されて見えなくなっても、障害物がなくなれば、再び物や人が見出されるはずだという認識をこの子どもは持っています。だから、ホームにさっきまで居た人が見えなくなったことに疑問を持ったのでしょう。しかし、この現象を「（ホームの人が）消えたよ」と表現していることから分かるように、電車の背後にいる人が、（子どもの）見えないところで移動する可能性のあることまでは認識していないのでしょう。こう考えてくると、この2歳児の物の永続性に関する認識はほぼ出来上がっているものの、自分の観察とは独立した物自体の移動を表象できるまでには至っていない水準の反応であると解釈できます。

もし、この解釈が正しいとすると、物が見えないところで移動したとき、物の移動を表象することは、乳児には難しいのではないか、という仮説を立てることができます。実際、同形同大の2つの不透明なコップを、その口を下にして子どもに提示し、一方のコップ（右のコップとしよう）の下におもちゃを隠す。次に、子どもの見ているところで、テーブルの上を滑らせるようにして左右のコップを入れ替えてから、おもちゃを探すように求める。コップの入れ替えによっておもちゃも左に移動するので、おもちゃは左のコップにあるにもかかわらず、乳児はおもちゃが最初に隠された右のコップ下を探そうとします。この課題が解決されるのもやはり2歳頃なのです。この課題においても、子どもは右のコップにおもちゃが隠されたこと、そのコップが左に移動したことを見ていますが、おもちゃ自体が右から左に異動したことは見ていません。移動後に右のコップの下を探して、おもちゃが見つからなかったとき、子どもは「どうしておもちゃが消えたの?」という疑問を懐いたことでしょう。この課題の結果も、物が見えないところで移動する可能性を認めることは乳児にはとても難しいことを示しています。

冒頭で紹介した2歳児と母親との会話はエピソード的資料ですから、私の解釈が正しいかどうか本当のところは分かりません。しかし、ここで問題にしたかったことは、この逸話をどう解釈するのが正しいかどうかではなく、日常のちょっとした逸話をきっかけとして面白い研究テーマが見つかるということです。そのような例をいくつか挙げてみましょう（いずれも、出典は朝日新聞の記事『あのね』からです）。

・例1：帰省したときのこと、セミを拾った祖父から「死んでいるからもう動かないんだよ」と教えられ、「電池が切れたの？」（3歳児）
・例２：工事現場で大きなクレーン車が長いアームを上に伸ばしていた。「大変! お空にぶつかっちゃうよ。とまれ！」（2歳児）
・例３：雪の降る寒い日。さしている傘から溶けた雪の水滴がぽたぽた落ちてきた。「寒いねぇ。傘も寒い寒いといって泣いているね」（4歳児）
・例４：テレビで昔の白黒画面を見て不思議がる息子に「お母さんが子どものころは白黒でしか映らなかったのよ」と言うと、「じゃあ、お母さんも子どもの時は白黒だったの？」（7歳児）
・例５：一万円札で110円の切符を買うとお釣りが出てきた。「ママ、お金いっぱいになって良かったね。なくなったらまた切符買えばいいよ」（3歳児）
・例６：「あのね、わたし赤ちゃん産まないの！」「なんで？」「ママがおばあちゃんになるから」（5歳児）

このような逸話について、単に子どもは比喩がうまいと感心したり、逆に、子どもは無知であるが故に大人を笑わせるというような感想で済まさないでください。子どもは真剣に考え、マジで答えているのですから、いずれの事例からも、子ども特有の思考様式を垣間見ることができるのです。例1は子どもの素朴生物学、例2は子どもの空間表象、例3は子どもの素朴自然認識、例4は子どもの映像認識、例5は子どもの経済的、量的認識、例6は子どもの社会的関係（と生物的関係）認識に関わっています。このような逸話をきっかけに、子どもの思考様式の解明という、認知発達研究への旅立ちが始まるのです。

4 確率課題

これまでの課題例は幼児あるいは児童に関するものですから、それらの課題に対して皆さんが同じような誤りをするというものではありませんでした。そのため、子どもの反応を知っても、「そんなものか」という印象で終わってしまったかもしれません。また、中学生以降の青年期の課題として当研究室でやっている研究の一つを紹介するという意味も込めて、次の問題を考えてみてください（当研究室院生の伊藤朋子さんの研究）。

問題1：さいころを振ったところ奇数の目が出ました。このとき、5の目が出ている確率はいくらですか。

皆さん、この問題は計算しなくてもできますから、次を読み進める前に、まずこの問題に回答してください。確率は1/6となったでしょうか、それとも1/3になったでしょうか。

・確率1/6と答えた人は、奇数の目が出る確率は1/2、そのうちで5が出る確率は1/3、したがって1/2×1/3＝1/6と考えます。
・確率1/3と答えた人は、奇数の目が出る確率は1/2、それに対し5が出る確率は1/6、したがって1/6÷1/2＝1/3と考えます。
皆さんはどちらが正しいと考えますか。そこで、次の問題を考えてください。

問題2：さいころを振ったところ1か3か5の目が出ました。このとき、5の目が出ている確率はいくらですか。

この問題に1/6と答えた人はいるでしょうか。おそらくほとんどの人は1/3と答えたのではないかと思います。しかし、表現に違いがあると言え、問題1と問題2とは同じ問題です。「奇数の目」という代わりに「1か3か5の目」と言っているだけです。にもかかわらず、問題1に対して1/3と答えることができる者は大学生でも半数ほどしかいないのです。残りの半数のほとんどが1/6と答えます。これはなぜでしょうか。皆さん自身が問題1に対して1/6と答えたのであれば、なぜそう答えてしまったのかを自問してください。1/3と答えたのであれば、なぜ大学生（大人）でも半数ほどは1/6と答えてしまうのかを、皆さん自身の問題解決過程を内省しながら、考えてください。

　少し問題を掘り下げると、問題１で求められていることは、条件確率Pr(5の目|奇数の目）です。これは条件確率の定義にしたがって、Pr(5の目&奇数の目）/ Pr(奇数の目）に等しく、したがってPr(5の目）/ Pr(奇数の目）に等しい。それゆえ、Pr(5の目|奇数の目）＝1/6÷1/2＝1/3となります。ところが、1/6と答えた者はPr(5の目）で、元をただせば、Pr(5の目&奇数の目）で答えていることになります。つまり、条件確率Pr(5の目|奇数の目）を連言確率Pr(5の目&奇数の目）と混同していることになります。あるいは、Pr(5の目&奇数の目）/ Pr(奇数の目）で答えるべきところをPr(5の目&奇数の目）で答えているわけですから、前者の分母Pr(奇数の目）を、つまり問題で与えられたデータを全く無視しているともいえます。この問題はデータの無視（data neglect）ともいわれ、データの無視はなぜ起こるのか、そもそも本当にデータを無視しているといえるのかといった問題として、現在の学界でも盛んに議論されているところです。

　また一方では、問題2で求められていることは、条件確率Pr(5の目|1か3か5の目）＝1/3ですから、「奇数の目」という代わりに「1か3か5の目」というように、奇数の意味を外延的に表示すれば、なぜかくも容易にこの問題に答えられるのか、という問題も提起されることになります。この問題は確率的推論における頻度表示の効果なのか、外延関係の明示の効果なのかという問題として、現在の学界においても盛んに議論されています。議論しているというよりバトルといったほうが相応しいほどの激しい論争です。ここでは論争の詳細には立ち入らないことにしましょう。ここで皆様にお伝えしたかったことは、問題1のような極々単純な確率課題の検討から出発しても、その要因の糸をたどって行けば、現在の学界の最前線で議論されている本質的問題に結びついてくるということです。そして、皆さんがこのような学界の最前線で活躍されることも決して夢ではないということをお伝えしたかったのです。

以上、認知発達現象に関して、皆さんに興味を持っていただけそうな事例をいくつか紹介しました。最後に強調しておきたいことは、このような研究を行なうのに、チンパンジーを探してアフリカのジャングルに分け入るような必要も、あるいは、目を凝らして顕微鏡下を覗き込むような必要もないという点です。皆さんの極く身近にいる乳児、幼児、児童、青年が汲めども尽きぬ感動と不思議の源泉であり、科学的研究テーマの宝庫であるという認識を持っていただきたいのです。